The main tool in calculating what will happen in collisions is knowing the conservation of momentum. You know that the total momentum before the collision is the same as the total momentum after the collision as long as there are no significant external forces.
When two objects collide (one is initially at rest and the other is moving), and you know the final velocity and mass of one object after the collision, you can calculate the final velocity of the other object. You can do this because the total momentum is conserved, so it’s the same, before and after the collision, as shown in this equation:
po = pf
Sample question
A pool ball with a mass of 170 g and a speed of 30 m/s hits another pool ball that’s at rest. If the first pool ball ends up going in the same direction with a speed of 10 m/s, what is the new speed of the second pool ball?
The correct answer is 20 m/s.
Use the equation po = pf.
All travel is in the same direction in this question, so you can treat it as a scalar equation. Find the original total momentum:
po = (0.17 kg)(30 m/s) = 5.1 kg-m/s
The original total momentum equals the total final momentum, which is given by this expression, where p2f is the final momentum of the second ball:
po = 5.1 kg-m/s = pf = (0.17 kg)(10 m/s) + p2f
Solve for p2f:
p2f = 5.1 kg-m/s – 1.7 kg-m/s = 3.4 kg-m/s
Divide p2f by the pool ball’s mass to find its speed:
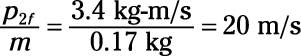
Practice questions
A 160-g hockey puck traveling at 60 m/s hits a stationary puck. If the first puck ends up going at 20 m/s in the same direction as the second puck, how fast is the second puck moving?
You’re driving a bumper car at an amusement park circus at 18 m/s, and you hit another car that’s at rest.
If you end up going at 6.0 m/s, what is the final speed of the other car, given that both cars have 100.0-kg mass, you have 80.0-kg mass, and the other person has a mass of 70.0 kg?
3.On the athletic field, a golf ball with a mass of 0.20 kg and speed of 100.0 m/s hits a soccer ball at rest that has a mass of 0.45 kg.
If the golf ball ends up at rest, what is the soccer ball’s final speed, given that it travels in the same direction as the golf ball was originally traveling?
You’re stopped at a traffic light when a 1,000.0-kg car (including driver) hits you from behind at 10.0 m/s. Ouch.
If the other car ends up moving at 6 m/s, and if you and your car have a mass of 940 kg, what is your final speed?
Following are answers to the practice questions:
58 m/s
Use the equation po = pf.
The pucks travel in the same direction here, so you can treat this as a scalar equation. Find the original total momentum:
po = (0.16 kg)(60 m/s) = 9.6 kg-m/s
This equals the total final momentum, which is given by this expression, where p2f is the final momentum of the second puck:
po = 9.6 kg-m/s = pf = (0.16 kg)(20 m/s) + p2f
Solve for p2f:
p2f = 9.6 kg-m/s – 0.32 kg-m/s = 9.28 kg-m/s
5.Divide p2f by the puck’s mass to find its speed:
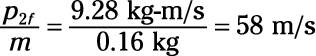
13 m/s
Use the equation po = pf.
The bumper cars travel in the same direction here, so you can treat this as a scalar equation. Find the original total momentum:
po = (18 m/s)(100.0 kg + 80.0 kg) = 3,240 kg-m/s
This equals the total final momentum, which is given by this expression, where p2f is the final momentum of the second bumper car:
po = 3,240 kg-m/s = pf = (100.0 kg + 80.0 kg)(6.0 m/s) + p2f
Solve for p2f:
p2f = 3,240 kg-m/s – 1,080 kg-m/s = 2,160 kg-m/s
Divide p2f by the bumper car and person’s mass to find its speed:

which rounds to 13 with,significant figures44 m/s
Use the equation po = pf.
Find the original total momentum:
po = (0.20 kg)(100.0 m/s) = 20 kg-m/s
This equals the total final momentum, which is given by this expression, where p2f is the final momentum of the soccer ball:
po = 20 kg-m/s = pf = p2f
Solve for p2f:
p2f = 20 kg-m/s
Divide p2f by the soccer ball’s mass to find its speed:
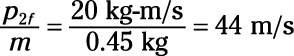
4.2 m/s
Use the equation po = pf.
Find the original total momentum:
po = (1,000.0 kg)(10.0 m/s) = 10,000 kg-m/s
This equals the total final momentum, which is given by the following expression, where p2f is the final momentum of the car:
po = 10,000 kg-m/s = pf = (1,000.0 kg)(6 m/s) + p2f
Solve for p2f:
p2f = 4,000 kg-m/s
Divide p2f by you and your car’s mass to find its speed:

